三角形——全等模型
答题习惯
一定要标注,用不同颜色的笔分组标记等角等边
主要模型类型
手拉手模型
三垂直模型(一线三等角)
中线倍长模型
全等辅助线之截长补短
半角模型(用截长补短做辅助线)
等补四边形模型
手拉手模型
模型讲解
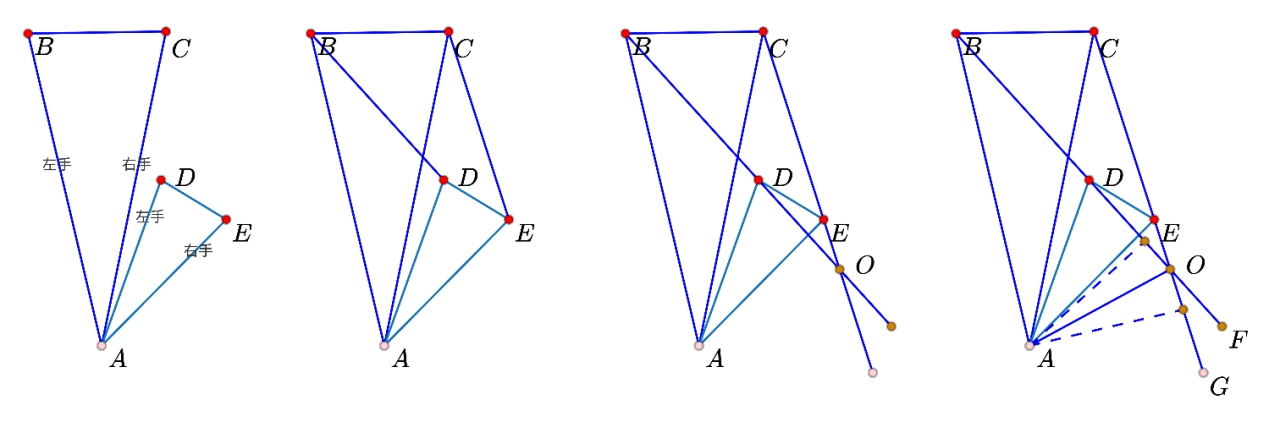
两个等腰三角形,共顶点,顶角相等。
如图一,
识别左右手连线,顶点与左右手连线构成的2个三角形全等。
如图二,顶点A与左手连线BD构成
,顶点A与右手连线构成 , 左右手连线相交产生2组对顶角(如果未相交,可以做延长让它们相交),其中有一组对顶角与等腰三角形顶角相等。
如图三,
证明思路:根据
, ,8字型 得出 部分顶角为直角的可以直接计算角度来证明
识别左右手连线的交点,交点与顶点的连线是角平分线
如图四,
平分 ,证明思路:过点 分别向 。两个垂线段分别是 的高,因为两三角形全等,所以面积与底都相等,所以高也相等,得出两垂线段相等,得出OA平分
典型例题:两等边三角形手拉手
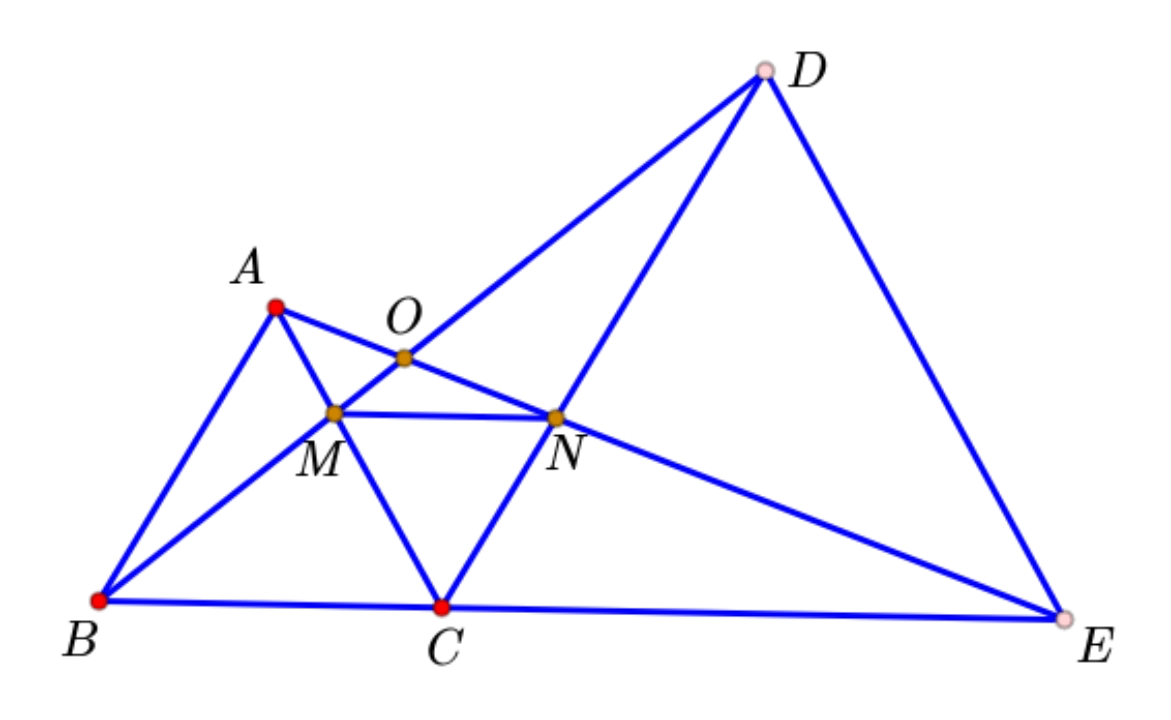
如图,
八大结论(证明并记住所有结论)
平分 是等边三角形
总结
模型识别技巧:首先找到公共顶点,简称头。然后依次找大图的左手,小图的左手,确认2个左手的连线。再找大图的右手,小图的右手,确认右手的连线。两个连线分别与顶点构成一组全等三角形(简记头左左
头右右)(SAS) 左手连线与右手连线形成的夹角,叫做拉手夹角,拉手夹角=顶角(“8”字形证明)
手拉手模型衍生出来的性质(边相等,角相等),可以与其他模型结合使用
三垂直模型(一线三等角)
模型构造:
- 一个等腰直角三角形
- 一条穿过等腰直角三角形顶点的直线(2种画法)
- 过两个底角顶点分别向直线做垂线段
模型结论:
- 全等:垂线段与顶点构成的2个三角形全等(AAS)
倍长中线
全等辅助线之截长补短
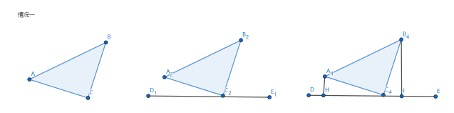
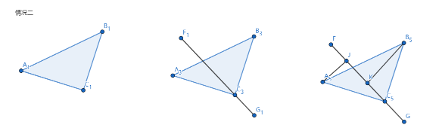
例题一
如图,在
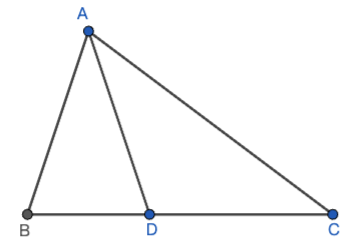
解析:对于这种求线段数量关系的题目,截长补短是常见的辅助线做法,在本题中,我们是求证AB、BD、AC三条线段之间的关系,首先确定AB、BD为短边,AC为长边。我们可以采取延长短边 或 截取长边两种辅助线做法。
补短法一,延长AB至点E,使BE=BD,连DE
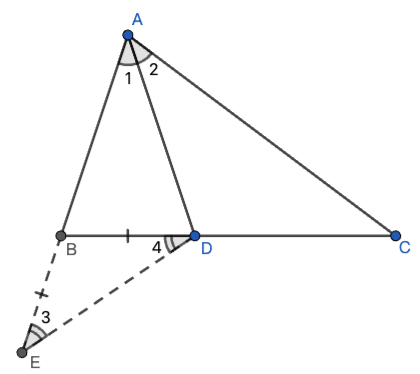
先证明
补短法二,延长DB至点E,使BE=AE,连DE
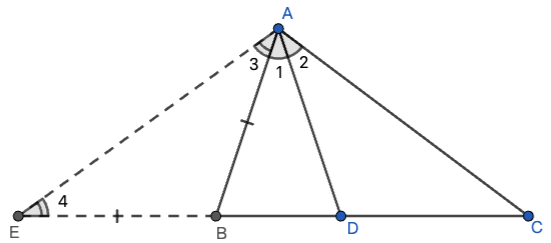
先证明
截长法一,在
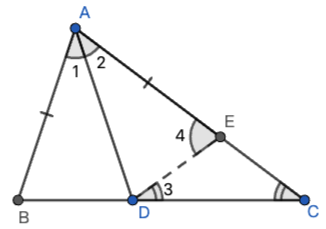
先证明
总结
从以上步骤可以看出,我们采取不同的截长补短策略,会直接影响到后续的解题思路和解题难度,在实际做题时,应通过分析寻找经可能简单的截长补短做法。
同时,也并不是所有的截长补短辅助线都能证明到题目需要的结论,部分题型是只有唯一的解法的。
半角模型
角平分线性质
- 构造全等,转移线段